Corrigé du 85 P. 76
retour
a.
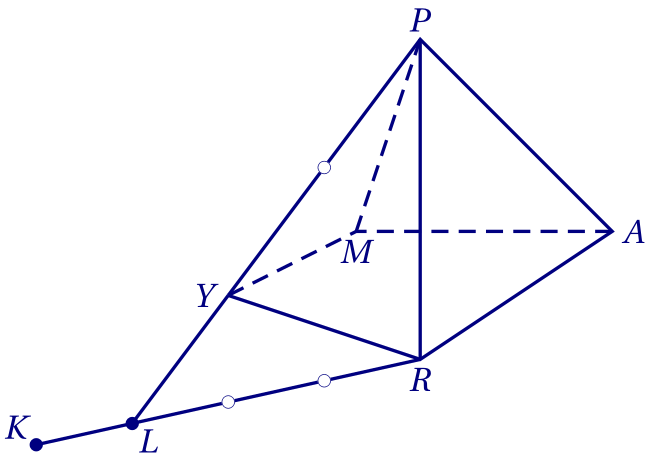
Pour placer le point $L$:
\begin{align*}
\overrightarrow{LP}&=3\overrightarrow{LY}&
\\ \iff
\overrightarrow{LP}&=3\left(\overrightarrow{LP}+\overrightarrow{PY}\right)&
\\ \iff
\overrightarrow{LP}&=3\overrightarrow{LP}+3\overrightarrow{PY}&
\\ \iff
\overrightarrow{LP}-3\overrightarrow{LP}&=3\overrightarrow{PY}&
\\ \iff
-2\overrightarrow{LP}&=3\overrightarrow{PY}&
\\ \iff
2\overrightarrow{PL}&=3\overrightarrow{PY}&
\\ \iff
\overrightarrow{PL}&=\frac 3 2 \overrightarrow{PY}.&
\end{align*}
Pour placer le point $K$:
\begin{align*}
4\overrightarrow{KL}-\overrightarrow{KR} &= \vec 0&
\\ \iff
4\left(\overrightarrow{KR}+\overrightarrow{RL}\right) - \overrightarrow{KR} &= \vec 0&
\\ \iff
4\overrightarrow{KR}+4\overrightarrow{RL}-\overrightarrow{KR}&=\vec 0&
\\ \iff
3\overrightarrow{KR} &= -4\overrightarrow{RL}&
\\ \iff
\overrightarrow{KR} &=-\frac 4 3\overrightarrow{RL}&
\\ \iff
\overrightarrow{RK} &= \frac 4 3 \overrightarrow{RL}.&
\end{align*}
b. (Méthode avec vecteurs.) Montrons que le point $K$ appartient au plan $(PYR)$, ce qui revient à trouver deux réels $\alpha$ et $\beta$ tels que \[\overrightarrow{PK} = \alpha\overrightarrow{PY}+\beta\overrightarrow{PY}.\] Donc: \begin{align*} \overrightarrow{PK} &=\overrightarrow{PR}+\overrightarrow{RK}& \\ &=\overrightarrow{PR}+\frac 4 3\overrightarrow{RL}& \\ &=\overrightarrow{PR}+\frac 4 3 \left(\overrightarrow{RP}+\overrightarrow{PL}\right)& \\ &=\overrightarrow{PR}+\frac 4 3\overrightarrow{RP} + \frac 4 3 \overrightarrow{PL}& \\ &=\overrightarrow{PR}-\frac 4 3\overrightarrow{PR}+ \frac 4 3 \left(\frac 3 2\overrightarrow{PY}\right)& \\ &=-\frac 1 3 \overrightarrow{PR} + 2\overrightarrow{PY}.& \end{align*} Donc le point $K$ appartient bien au plan $(PYR)$ et donc $P$, $Y$, $R$ et $K$ sont coplanaires.
b. (Méthode sans vecteurs.)
Montrons que $K$ appartient au plan $(PYR)$.
La relation $\overrightarrow{PL}=\dfrac 3 2 \overrightarrow{PY}$ montre que le point $P$ appartient à la droite $(PY)$.
Or cette droite est incluse dans le plan $(PYR)$, et par conséquent $L$ appartient à $(PYR)$.
Puisque $L$ et $R$ appartiennent à $(PYR)$, la droite $(RL)$ entière appartient à ce plan.
Or la relation $\overrightarrow{RK}=\dfrac 4 3\overrightarrow{RL}$ montre que $K$ appartient à cette droite et donc au plan $(PYR)$.
retour