Corrigé du 62 P. 74

retour

1.

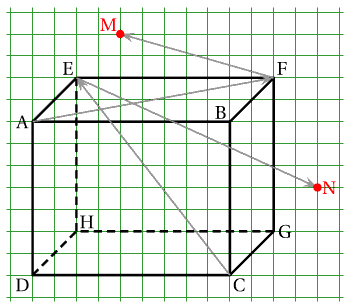
2.a. Utilisons la relation qui définit $\overrightarrow{AM}$ puis décomposons selon les directions des arêtes du cube en utilisant la relation de Chasles. \[\begin{aligned} \overrightarrow{AM} &=\overrightarrow{AF} + \overrightarrow{BE}& \\ &=\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{BF}+\overrightarrow{FE}& \\ &=\overrightarrow{AB}+\overrightarrow{FE}+2\overrightarrow{BF}.& \end{aligned}\] Or $\overrightarrow{FE}=-\overrightarrow{AB}$ donc: \[\overrightarrow{AM}=\overrightarrow{AB}-\overrightarrow{AB}+2\overrightarrow{BF}=2\overrightarrow{BF}.\] Enfin, $\overrightarrow{BF}=\overrightarrow{AE}$ donc finalement: \[\overrightarrow{AM}=2\overrightarrow{AE}.\]

2.b. Procédons de même ici: \[\overrightarrow{CN} =\overrightarrow{CE}+\overrightarrow{AG} =\overrightarrow{CD}+\overrightarrow{DA}+\overrightarrow{AE} +\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CG}.\] Or $\overrightarrow{AB}=-\overrightarrow{CD}$, $\overrightarrow{BC}=-\overrightarrow{DA}$ et $\overrightarrow{CG}=\overrightarrow{AE}$, donc \[\overrightarrow{CN}=2\overrightarrow{CG}.\]

3.a. $\overrightarrow{EM} = \overrightarrow{EA}+\overrightarrow{AM} =\overrightarrow{EA}+2\overrightarrow{AE} =\overrightarrow{AE}$.
$\overrightarrow{GN}= \overrightarrow{GC}+2\overrightarrow{CG} =\overrightarrow{CG}$.
Mais $\overrightarrow{AE}=\overrightarrow{CG}$ donc \[\overrightarrow{EM}=\overrightarrow{GN}.\]

3.b. On en déduit que $EMNG$ est un parallélogramme.

retour