Corrigé du 11 P. 61

retour

■ 1.

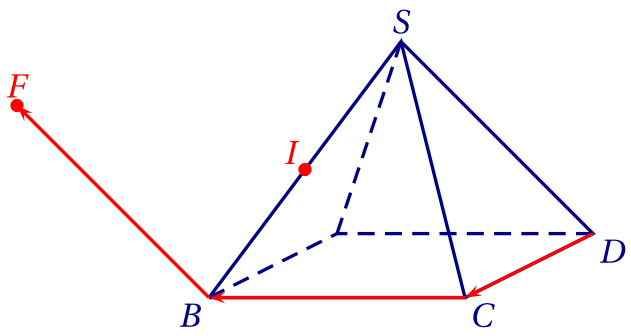
2 On peut écrire que: \[\begin{aligned} \overrightarrow{DI} &=\overrightarrow{DA}+\overrightarrow{AI}& \\ &=\overrightarrow{DA}+\frac 1 2 \overrightarrow{AB}& \\ &=\overrightarrow{DA}+\frac 1 2 \left( \overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CB} \right)& \\ &=\overrightarrow{DA}+\frac 1 2 \overrightarrow{AD} +\frac 1 2 \overrightarrow{DC} + \frac 1 2 \overrightarrow{CB}& \\ &=\frac 1 2 \overrightarrow{DA}+\frac 1 2 \overrightarrow{DC} +\frac 1 2 \overrightarrow{CB}& \\ &=\frac 1 2 \overrightarrow{DA}+ \frac 1 2 \overrightarrow{DC} +\frac 1 2 \overrightarrow{DE}.& \end{aligned}\]

3. On a donc: \[\begin{aligned} \overrightarrow{DI} &=\frac 1 2 \overrightarrow{DA} + \frac 1 2 \overrightarrow{DC} +\frac 1 2 \overrightarrow{DE}& \\ &=\frac 1 2 \left(\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{DE} \right)& \\ &=\frac 1 2 \overrightarrow{DF}.& \end{aligned}\] On en déduit que $I$ est le milieu de $[DF]$.

retour