Corrigé du 10 P. 61
retour
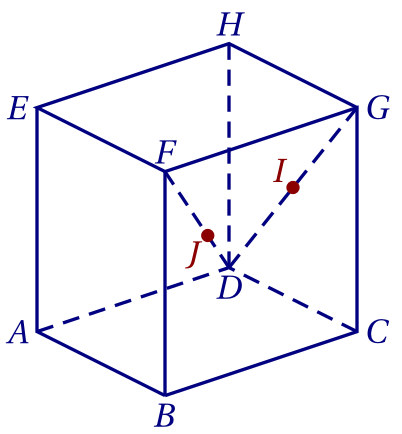
■ 1. Voir ci-contre
2.a.
☛On fait d'abord apparaître le vecteur $\overrightarrow{DJ}$ car il a servi à construire le point $J$.
\[\overrightarrow{HJ} = \overrightarrow{HD}+\overrightarrow{DJ}
=\overrightarrow{HD}+\frac 1 3 \overrightarrow{DF}.\]
☛On décompose les vecteurs selon les directions des arêtes du cube.
\[\begin{aligned}
\overrightarrow{HJ}
&=
\overrightarrow{HD}+\frac 1 3 \left(\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BF}\right)&
\\
&=\overrightarrow{HD}+\frac 1 3 \overrightarrow{DC}+\frac 1 3 \overrightarrow{CB} + \frac 1 3\overrightarrow{BF}&
\end{aligned}\]
☛On substitue les représentants de certains vecteurs.
Ici $\overrightarrow{CB}=\overrightarrow{DA}$ et $\overrightarrow{BF}=-\overrightarrow{HD}$.
\[\begin{aligned}
\overrightarrow{HJ}
&=\overrightarrow{HD}+\frac 1 3\overrightarrow{DC} + \frac 1 3 \overrightarrow{DA} - \frac 1 3 \overrightarrow{HD}&
\\
&=\frac 2 3 \overrightarrow{HD} + \frac 1 3 \overrightarrow{DC} + \frac 1 3\overrightarrow{DA}&
\\
&=-\frac 2 3 \overrightarrow{DH}+\frac 1 3 \overrightarrow{DC}+ \frac 1 3 \overrightarrow{DA}.&
\end{aligned}\]
2.b. ☛La méthode reste la même. \begin{align*} \overrightarrow{AJ} &=\overrightarrow{AD} + \overrightarrow{DJ}& \\ &=\overrightarrow{AD} +\frac 1 3 \left( \overrightarrow{DA}+\overrightarrow{AB}+\overrightarrow{BF} \right)& \\ &=\overrightarrow{AD}+\frac 1 3 \overrightarrow{DA} +\frac 1 3\overrightarrow{AB} + \frac 1 3 \overrightarrow{BF}& \\ &=\frac 2 3 \overrightarrow{AD} + \frac 1 3 \overrightarrow{AB} +\frac 1 3 \overrightarrow{BF}& \\ &=\frac 2 3 \overrightarrow{AD} + \frac 1 3 \overrightarrow{DC} +\frac 1 3 \overrightarrow{DH}& \\ &=-\frac 2 3 \overrightarrow{DA} + \frac 1 3 \overrightarrow{DH} +\frac 1 3 \overrightarrow{DC}.& \end{align*}
3. ☛Puisque $I$ est le milieu de $[GD]$, il faut faire apparaître le point $D$ (ou le point $G$). \[\overrightarrow{AI} = \overrightarrow{AD} + \overrightarrow{DI} =\overrightarrow{AD} + \frac 1 2 \overrightarrow{DG}.\] ☛On décompose alors selon les directions des arêtes du cube (représentées justement par les vecteurs $\overrightarrow{DA}$, $\overrightarrow{DC}$ et $\overrightarrow{DH}$). \[\overrightarrow{AI} = \overrightarrow{AD} + \frac 1 2 \left(\overrightarrow{DH}+\overrightarrow{HG}\right) =-\overrightarrow{DA} + \frac 1 2 \overrightarrow{DH} +\frac 1 2 \overrightarrow{DC}.\]
4. On peut remarquer que: \[\begin{aligned} \frac 3 2 \overrightarrow{AJ} &=\frac 3 2 \left( -\frac 2 3 \overrightarrow{DA} + \frac 1 3 \overrightarrow{DH} +\frac 1 3 \overrightarrow{DC}\right)& \\ &=-\overrightarrow{DA}+\frac 1 2 \overrightarrow{DH} + \frac 1 2 \overrightarrow{DC}& \\ &=\overrightarrow{AI}.& \end{aligned}\] Puisque $\overrightarrow{AI}=\frac 2 3 \overrightarrow{AJ}$, ces vecteurs sont colinéaires donc les points $A$, $I$ et $J$ sont alignés.
retour