Corrigé du 71 P. 43

retour

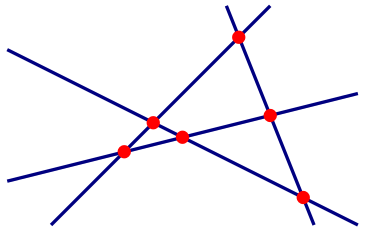
1. Il y a autant de points d'intersection que de paires de droites possibles. Donc avec six droites, on aura \[\binom{4}{2} = \frac{4\times 3} 2 = 6\ \text{points}.\] On peut confirmer cette réponse avec la figure ci-dessous.

2.a. $\displaystyle\binom{5}{2} = \dfrac{5\times 4} 2 = 10$;

2.b. $\displaystyle\binom{6}{2} = \dfrac{6\times 5} 2 = 15$;

2.c. $\displaystyle\binom{15}{2} = \dfrac{15\times 14} 2 = 105$.

3. Notons $u_n$ le nombre de régions obtenues avec $n$ droites.
Avec aucune droite, on a une région, donc $u_0 = 1$.
Avec une droite, on a deux régions donc $u_1 = 2$.
Avec deux droites, on a $u_2 = 4$ régions, etc.
S'il y a déjà $n$ droites dessinées, le tracé de la $n+1$-ième droite va couper $n+1$ régions, donc créer $n+1$ nouvelles régions.

La suite $(u_n)$ vérifie donc la relation de récurrence : \[\forall n\in\mathbb N, u_{n+1} = u_n + (n+1).\] Alors :

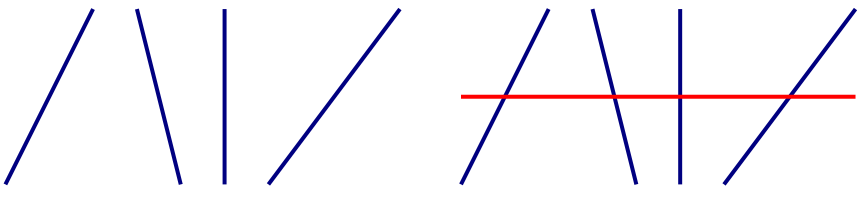
3.a. $u_3 = u_2 + 3 = 4+3 = 7$ donc $u_4 = u_3 + 4 = 7+4 = 11$.

3.b. $u_5 = u_4 + 5 = 11 + 5 = 16$.

3.c. On peut remarquer que \[\begin{aligned} u_n &= n + u_{n-1}& \\ &= n + (n-1) + u_{n-2}& \\ &= n + (n-1) + \cdots + 1 + u_0& \\ &= n + (n-1) + \cdots 1 + 1& \\ &=\frac{n(n+1)}2 + 1. \end{aligned}\] Donc $u_{15} = \dfrac{15\times 16}2 + 1 = 121$.

retour