Corrigé du 69 P. 43

retour

1. Un code est un triplet de $C = \{0,1,\cdots,9\}$. $\operatorname{card}(C) = 10$ donc le nombre de codes possibles est \[\operatorname{card}(C^3) = 10^3 = 1000.\]

2.a. $\operatorname{card}(\{000, 111, \cdots , 999\}) = 10$.

2.b. Un tel code est un triplet de $P^3$ où $P=\{0;2;4;6;8\}$. Donc leur nombre est \[\operatorname{card}(P^3) = 5^3 = 125.\]

2.c. Les chiffres premiers forment l'ensemble $E=\{2; 3; 5; 7\}$ de cardinal 4. Donc \[\operatorname{card}(E^3) = 4^3 = 64.\]

2.d. Pour concevoir un tel code, on peut successivement :

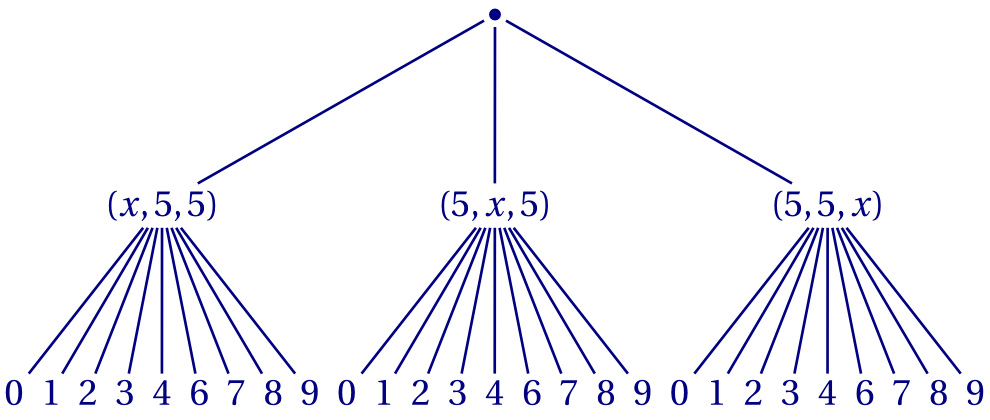
• Choisir la position du chiffre différent de 5 (il y en a 3 possibles: $(x,5,5)$, $(5,x,5)$ ou $(5,5,x)$).
• Puis choisir le chiffre différent de 5 (il y a donc 9 choix possibles).

Le nombre de codes possibles est donc : $3\times 9 = 27$.

retour