Corrigé du 66 P. 43

retour

On peut modéliser la situation à l'aide d'un diagramme de Venn, dans lequel $F$ est l'ensemble des animaux de la ferme, $L$ celui des lapins, $B$ celui des animaux blancs et $V$ celui des animaux vaccinés.

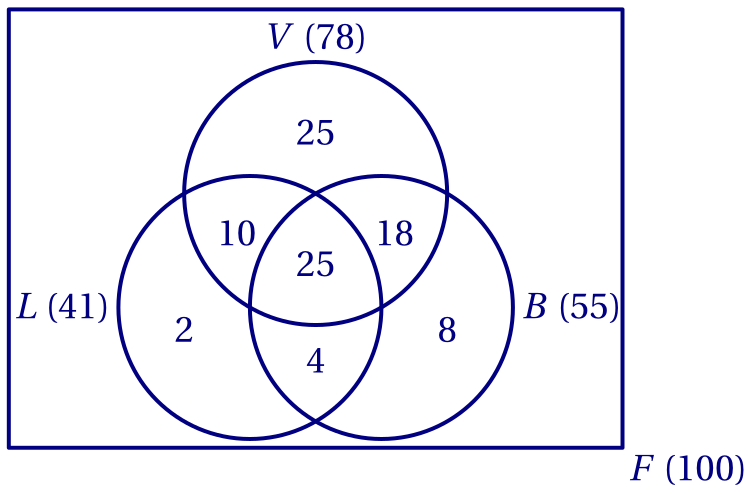
Construction : On place 25 à l'intersection des trois ensembles puis \begin{align*} &35 - 25 = 10& &43 - 25 = 18& \\ &29 - 25 = 4& &41 - 10 - 25 - 4 = 2& \\ &55-4-25-18 = 8& &78-10-25-18 = 25& \end{align*}

a. Il y a donc $\operatorname{card}((L\cap B)\setminus V) = 4$ lapins blancs non vaccinés.

b. On a : \[\operatorname{card}(L\cup B\cup V) = 2+10+25+4+18+8+25 = 92.\] Donc le nombre d'animaux qui ne sont ni des lapins, ni blancs ni vaccinés est : \[\operatorname{card}(F\setminus(L\cup B\cup V)) = 100 - 92 = 8.\]

retour