Corrigé du 65 P. 43

retour

On note $E=\{0; 1; 2;\ldots;6\}$ avec $\operatorname{card}(E) = 7$.

Première méthode. Les dominos sont des paires de deux éléments pris dans $E$.
Puisqu'il n'y a pas de considérations d'ordre entre les deux éléments de la paire, on peut décider qu'on les désignera toujours avec le premier numéro supérieur ou égal au second.
l'arbre ci-dessous permet de les dénombrer tous:

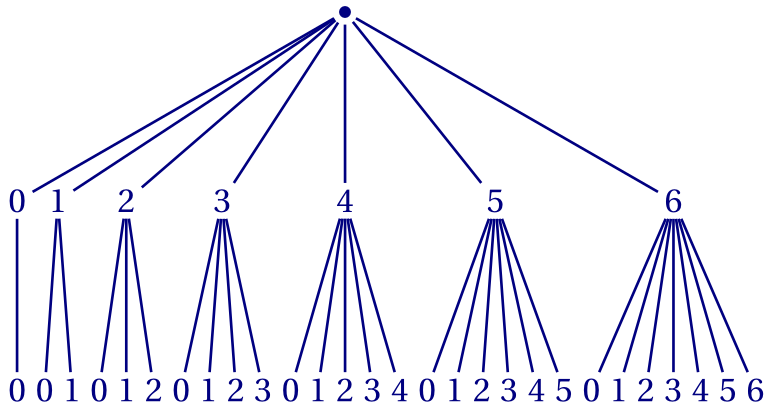
Donc le nombre de dominos possibles est \[1+ 2 + 3 + \cdots + 7 = \frac{7 \times 8} 2 = 28.\]

Deuxième méthode. Parmi les dominos, il y a sept "doubles" (double vide, double un, double deux… jusqu'à double 6).
Tous les autres dominos sont des parties de deux éléments de l'ensemble $E$. Il y en a donc : \[\binom{7}{2} = \frac{7\times 6} 2 = 21.\] Cela fait au total 7+21 = 28 dominos.

retour