Corrigé du 63 P. 42
retour
a.
■ Modélisation 1. Si $C$ est l'ensemble des cadeaux, le problème revient à choisir toutes les parties possibles de $C$
pour Agathe
(Bastien obtenant les éventuels autres cadeaux).
Puisque $\operatorname{card}(C) = 3$, le nombre de choix possibles est $2^3 = 8$.
■ Modélisation 2. Si $E$ est l'ensemble des enfants, les répartitions de cadeaux sont des triplets de $E^3$, chaque
élément du triplet déterminant qui reçoit le cadeau correspondant.
Par exemple,
(A,B,B) est la situation où Agathe reçoit le premier cadeau et Bastien les deux autres.
Dans ce cas, le nombre de répartitions est
\[\operatorname{card}(E^3) = 2^3 = 8.\]
On peut retrouver ce dernier résultat à l'aide d'un arbre.
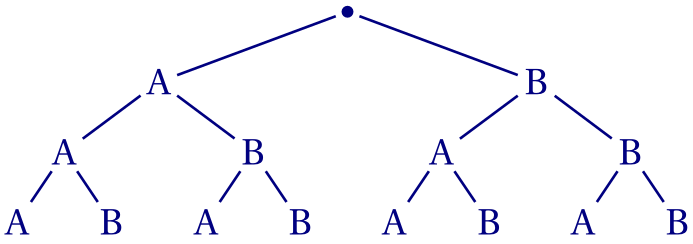
b. Soit $E$ l'ensemble des trois enfants. Les répartitions de cadeaux possibles sont des quintuplés de $E^5$: \[\operatorname{card}(E^5) = 3^5 = 243.\] (Il n'est plus envisageable ici de faire un arbre !)
c.
On peut "imaginer" un quatrième enfant qui reçoit les cadeaux que les trois autres n'ont pas eu.
Dans ce cas, une répartition de cadeaux est un quintuplé d'élément de $E'$ qui contient les quatre enfants.
Le nombre de répartitions possibles est alors :
\[\operatorname{card}(E') = 4^5 = 1024.\]
Méthode plus laborieux ! Il y a une façon de ne distribuer aucun cadeau. Si je distribue un seul cadeau,
j'ai cinq choix pour le cadeau, puis trois choix pour l'enfant à qui je le donne, et ainsi de suite...
Cela conduit à la formule :
\[{\small 1 + 5\times 3 + \binom{5}{2}\times 3^2 + \binom{5}{3}\times 3^3 + \binom{5}{4} \times 3^4 + \binom{5}{5}\times 3^5}
= 1024.\]
retour