Corrigé du 57 P. 299

retour

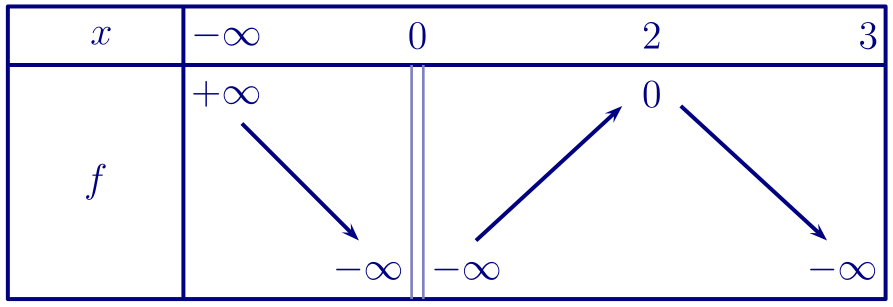
a. $\ln(u(x))$ n'existe que si et seulement si $u(x) > 0$.
Donc, d'après la courbe: $I = ]-\infty;0[\cup]0;3[$.

b. D'après la courbe, $\displaystyle\lim_{x\to-\infty} u(x) = +\infty$.
On sait d'autre part que $\displaystyle\lim_{X\to+\infty} \ln(X) = +\infty$.
Donc en composant ces limites : $\displaystyle\lim_{x\to-\infty} \ln(u(x)) = +\infty$.
 
De $\displaystyle\lim_{x\to 0} u(x) = 0$ et $\displaystyle\lim_{X\to 0} \ln(X) = -\infty$, on déduit par composition que \[\lim_{x\to 0} \ln(u(x)) = -\infty.\]
 
De $\displaystyle\lim_{\substack{x\to 3\\x < 3}} u(x) = 0$ et $\displaystyle\lim_{X\to 0} \ln(X) = -\infty$, on déduit par composition que \[\lim_{x\to 3} \ln(u(x)) = -\infty.\]

c. $\ln(X) = 0$ si et seulement si $X = 1$. Donc : \[ \ln(u(x)) = 0 \iff u(x) = 1. \] D'après la courbe, $S = \big\{-1;2\big\}$.
Ce sont donc les points de coordonnées $(-1;0)$ et $(2;0)$.

d. La fonction $x\mapsto \ln(x)$ étant strictement croissante, les variations de $f$ sur $I$ sont celles de la fonction $u$.

retour