Corrigé du 163 P. 182
retour
a.
À l'étape 0, on a un carré plein de côté 1, donc $u_0 = 4$.
À l'étape 1, on divise le carré en 9 carrés de côté 1/3, et on enlève le carré central, ce qui ajoute pour frontière le périmètre dudit carré.
\[u_1 = u_0 + 4\times \frac 1 3 = 4 + \frac 4 3 = \frac{12}3 + \frac 4 3 = \frac{16}3.\]
A l'étape 2, on divise les 8 carrés restants en 9, chaque nouveau carré mesurant le tiers du précédent, donc (1/3)²m.
On enlève 8 de ces nouveaux carrés, ce qui donne:
\[u_2 = u_1 + 8 \times 4 \times \left(\frac 1 3\right)^2 = \frac{16}3 + \frac{32}9 = \frac{48}{9}+\frac{32}{9} = \frac{80}9.\]
b.
À chaque étape, on multiplie par 8 le nombre de carrés à enlever. À l'étape 0, il faudra enlever $8^0=1$ carré pour passer à l'étape $1$,
à l'étape 1 il faudra enlever $8^1$ carrés pour passer à l'étape 2, etc…
À l'étape $n$, on enlèvera $8^n$ carrés pour passer à l'étape $n+1$.
La taille de ces carrés est divisée par 4 à chaque étape. A l'étape 0 (pour passer à l'étape 1), on enlève des carrés de taille $\dfrac 1 3$,
à l'étape 1 on enlève des carrés de taille $\left(\dfrac 1 3\right)^2$, et ainsi de suite.
Donc pour passer de l'étape $n$ à l'étape $n+1$, on enlève des carrés de taille $\left(\dfrac 1 3\right)^{n+1}$.
On a la relation:
\begin{align*}
u_{n+1} &= u_n + 4 \times 8^n \times \left(\frac 1 3\right)^{n+1}&
\\
&=u_n + \frac{4 \times 8^n \times 1}{3^{n+1}}&
\\
&=u_n + \frac{4 \times 8^n}{3\times 3^n}&
\\
&=u_n + \frac 4 3 \times \left(\frac 8 3\right)^n.&
\end{align*}

On peut ensuite utiliser cette fonction dans la console:
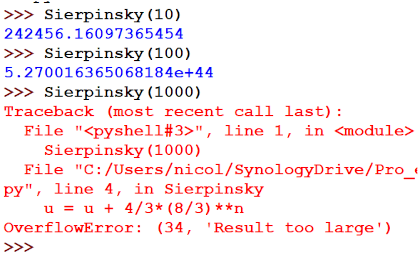
On voit que $u_{10}\approx 242\:456$, $u_{100} \approx 5,27\times 10^{44}$ et que $u_{1000}$ dépasse les capacités de calcul de la machine!
On peut donc conjecturer que $\displaystyle\lim_{x\to+\infty} u_n = +\infty$.
d.
Soit $\mathcal P(n)$ la proposition $u_n = \dfrac{16}5 + \dfrac 4 5\times \dleft(\frac 8 3\right)^n$.
Initialisation. Pour $n=0$:
\[\frac{16}5 + \frac 4 5 \left(\frac 8 3\right)^0 = \frac{16}5 + \frac 4 5\times 1 = \frac{20} 5 = 4 = u_0.\]
Hérédité. Supposons $\mathcal P(n)$ vraie pour $n$ donné. Alors:
\begin{align*}
u_{n+1} &= u_n + \frac 4 3 \times \left(\frac 8 3\right)^n&
\\
&=\frac{16}5 + \frac 4 5 \times \left(\frac 8 3\right)^n + \frac 4 3 \times \left(\frac 8 3\right)^n&
\\
&=\frac{16}5 + \left(\frac 8 3\right)^n \times \left[\frac 4 5 + \frac 4 3\right]&
\\
&=\frac{16}5 + \left(\frac 8 3\right)^n \times \left[\frac{12}{15}+\frac{20}{15}\right]&
\\
&=\frac{16}5 + \left(\frac 8 3\right)^n \times \frac {32}{25}&
\\
&=\frac{16}5 + \left(\frac 8 3\right) \times \frac{8}{3}\times \frac{4}{5}&
\\
&=\frac{16}5 + \left(\frac 8 3\right)^{n+1} \times \frac 4 5.&
\end{align*}
Donc $\mathcal P(n+1)$ est aussi vraie.
Conclusion. Par récurrence, pour tout entier naturel $n$, $\mathcal P(n)$ est vraie.
e. Puisque $\dfrac 8 3 > 1$, on sait que \[\lim_{n\to+\infty} \left(\frac 8 3\right)^n = +\infty.\] On en déduit que: \[\lim_{n\to+\infty} u_n = +\infty.\]
retour