retour

1. Puisque $(v_n)$ est géométrique de raison $q$, pour tout entier naturel $n$: \[v_n = v_0 q^n.\] Donc, en particulier: \[\begin{aligned} v_7 &= v_0 q^7& \\ \iff 2002 &= 800 \times q^7& \\ \iff \frac{2002}{800} &= q^7& \\ \iff 2,5025 &= q^7.& \end{aligned}\] Nous ne disposons pas de moyen de déterminer $q$ de manière exacte. Donc on peut faire des essais.
   
   On constate que : \[1,140^7 \approx 2,5023\;;\qquad 1,141^7 \approx 2,5177.\] Donc on peut admettre que $q\approx 1,14$.
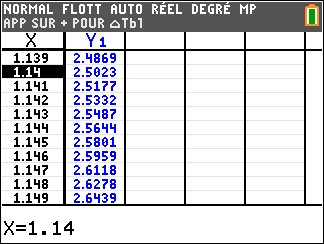
2. On a donc, pour tout entier naturel $n$: \[v_n = v_0q^n = 800 \times 1,14^n.\]
3. Si $n = 7$ : \[v_7 = 800 \times 1,14^7 \approx 2002.\]
4.   \[\begin{aligned} v_0 + v_1 + \cdots + v_{15} &= v_0\times \frac{1-q^{15+1}}{1-q}& \\ &=800 \times \frac{1-1,14^{16}}{1-1,14}& \\ &\approx 40\:784.& \end{aligned}\] On pouvait obtenir ce résultat à l'aide du programme Python ci-dessous.
   S = 0 for n in range(16) : S = S + 800*1.14**n print("somme =", S)
5. Nous avons obtenu un total de 40 784 éoliennes quand l'entreprise en annonce environ 40 000. Notre modélisation de la production par une suite géométrique semble donc pertinente.

retour

code : 30