37P23

retour

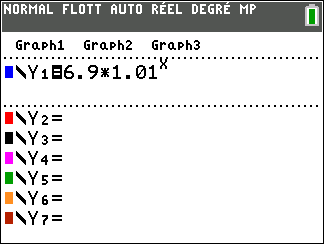
1. Si chaque année, la population augmente de 1%, chaque année la population est multipliée par \[1 + \frac 1 {100} = 1+0,01 = 1,01.\] Donc, pour tout entier naturel $n$, \[u_{n+1} = u_n \times 1,01.\] La suite $(u_n)$ est donc géométrique de raison $q=1,01$ et de premier terme $u_0=6,9$ (milliards d'habitants).
2. On en déduit que pour tout entier naturel $n$: \[u_n = u_0q^n = 6,9\times 1,01^n.\]
3. En 2025, $n = 2025 - 2010 = 15$. Or \[u_{15} = 6,9\times 1,01^{15} \approx 8,01.\] En 2025, la population avoisinera les 8 milliards.
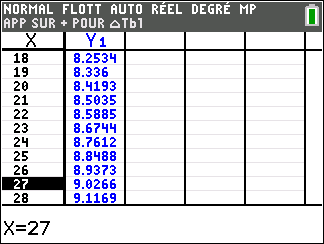
4. Poursuivons les calculs: \[\begin{aligned} u_{16} &= 6,9\times 1,01^{16} \approx 8,09& \\ &\ldots& \\ u_{26} &=6,9\times 10^{26} \approx 8,94& \\ u_{27} &=6,9\times 10^{27} \approx 9,03.& \end{aligned}\] Les 9 milliards d'individus seront donc atteint en 2010+27 = 2037.