64 P. 135

retour

1.a. Arbre:

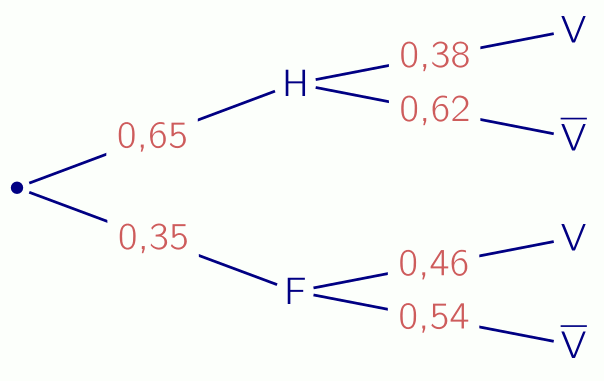
1.b. On cherche: \[P(\mathrm H\cap \mathrm V) =0,65 \times 0,38 =0,247.\]

1.c. On cherche: \[\begin{aligned} P(\mathrm V) &=P(\mathrm V \cap \mathrm H) + P(\mathrm V \cap \overline{\mathrm H})& \\ &=0,247 + 0,35\times 0,46& \\ &=0,247 + 0,161& \\ &=0,408.& \end{aligned}\]

1.d. Cherchons la probabilité, sachant que le client a acheté une voiture, que ce client soit un homme. \[ P_{\mathrm V}(\mathrm H) =\frac{P(\mathrm H \cap \mathrm V)}{P(\mathrm V)} =\frac{0,247}{0,408} \approx 0,605. \] Il y a environ 60% de chance qu'un client qui achète une voiture soit un homme, donc oui, plus de la moitié des acheteurs sont des hommes.

2.a. Arbre de probabilités:

2.b. «Deux clients achètent la voiture» est l'événement $\mathrm V_1\cap\mathrm V_2$.
Sa probabilité est donc: \[ P(\mathrm V_1\cap\mathrm V_2) =0,408^2 \approx 0,166. \]

2.c. L'événement «au moins un client achète la voiture» a pour événement contraire $\mathrm{\overline V_1}\cap\mathrm{\overline V_2}$, dont la probabilité est \[ P(\mathrm{\overline V_1}\cap\mathrm{\overline V_2}) = 0,592^2. \] Notre événement a donc pour probabilité: \[1 - 0,592^2 \approx 0,650.\]

retour

code : 135064