47 P. 133

retour

En notant $R_i$ l'événement « le stagiaire réussit la $i$-ème épreuve », on peut modéliser la situation à l'aide de l'arbre suivant.

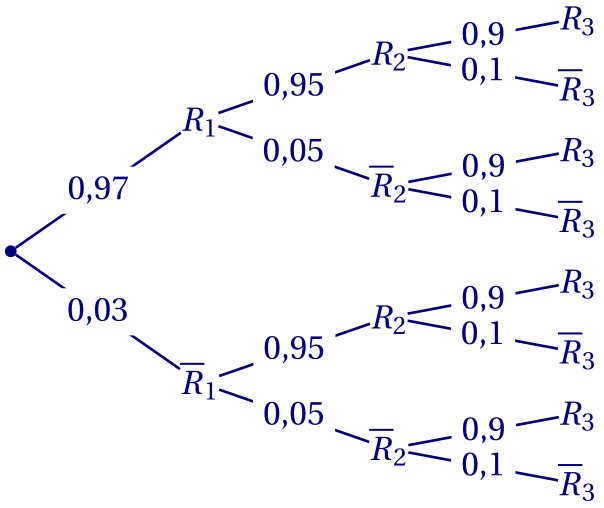
1. Probabilité que le stagiaire réussisse les trois épreuves: \[P(R_1\cap R_2 \cap R_3) = 0,97 \times 0,95 \times 0,9 = 0,82935.\]

2. Probabilité que le stagiaire échoue aux trois épreuves: \[P(\overline R_1 \cap \overline R_2 \cap \overline R_3) =0,03 \times 0,05 \times 0,1 = 0,00015.\]

3. Probabilité que le stagiaire réussisse exactement une épreuve: \begin{align*} &P(R_1 \cap \overline R_2 \cap \overline R_3) +P(\overline R_1 \cap R_2 \cap \overline R_3) +P(\overline R_1 \cap \overline R_2 \cap R_3)& \\= &{\small 0,97\times 0,05 \times 0,1 + 0,03 \times 0,95 \times 0,1 + 0,03 \times 0,05 \times 0,9}& \\= &0,00485 + 0,00285 + 0,00135 = 0,00905.& \end{align*}

retour

code : 133047