36 P. 131

retour

1. On peut proposer l'arbre suivant.

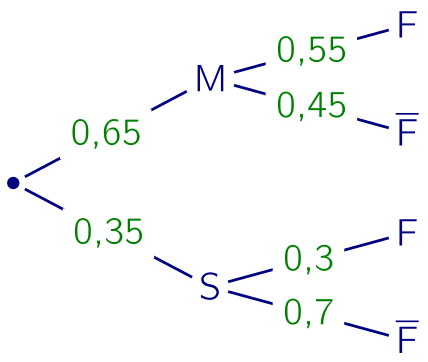
2. M∩F est l'événement «le client choisi vient le midi et il prend la formule entrée-plat-dessert».
Sa probabilité est \[P(\mathrm M \cap \mathrm F) = 0,65 \times 0,55 = 0,3575.\]

3. Un client qui prend la formule peut venir soit le midi, soit le soir. Donc \[\begin{aligned} P(\mathrm F) &=P(\mathrm M \cap \mathrm F) + P(\mathrm S \cap \mathrm F)& \\ &=0,3375 + 0,35\times 0,3& \\ &=0,3375 + 0,105& \\ &= 0,4625.& \end{aligned}\]

4. Il s'agit de trouver $P_{\mathrm F}(\mathrm M)$. D'après la définition: \[P_{\mathrm F}(\mathrm M) =\frac{P(\mathrm M\cap\mathrm F)}{P(\mathrm F)} =\frac{0,3375}{0,4625} \approx 0,773. \]

retour

code : 131036